To get started, 3D math is the study of the math behind the geometry of a 3D scene. 3D math involves applications with computers to model 3D worlds. These 3D worlds could be anything from 3D animations, cinematography, virtual reality, computer games, computer graphics, robotics, simulation, and much more.
This series of articles over the next few weeks will cover the theory and the practice of using mathematics specifically geometry in creating these 3D worlds. Later on, in the series, you will be shown how to convert the ideas learned here into C++ code.
It is important to note that the same concepts that are learned here can also be applied to other programming languages. If you are familiar with the concepts here you might want to jump straight ahead to part 2 of this 3D math series for computer graphics.
Getting Started with 3D Math
Before we dive right into this topic of 3D math you might want to know that I have made an assumption that you have some knowledge of geometry and basic algebra.
Exposure to trigonometry will also be an added advantage and make the process much more pleasant than for the rest of the readers.
Understanding The Cartesian Plane
Just like you were starting out to learn how to count you began with the number one. Likewise, I will do the same. As we begin to understand the coordinates that make up the Cartesian plane we need to first understand the three dimensions that make up 3D Worlds.
You may be familiar with the 1D component of 3D worlds as a number line.

The number line is simply that ruler-like line we are familiar with in mathematics that represents rational numbers. Basically rational numbers are numbers that can be counted as opposed to real numbers which might include numbers that really can’t be counted. like PI.
Anyway, the number line is a simple yet innovative representation of countable numbers in relation to each other with the center or the origin point being the number zero.
Zero is the point of origin in that, to the right of zero you have the positive numbers increasing as you move further from zero. How far? Infinite.
On the left side of the zero on the number line, you then have the reciprocal of the positive numbers. That is negative numbers. In the same way, as you move further away from the number line to the left the numbers decrease in value.
The 1D or the X-axis
Great. Now that we have that settled, it is also important to note that for this number line to represent the 1D representation of the 3D world it is usually placed and laid flat horizontally in relation to our viewpoint.
Some of you may argue that this is not entirely true. Sure enough. You are absolutely right. But stick with me, I will get into that later but for now, let us pretend that what I have said about the placement is correct.
Now that we have agreed on the placement of the 1D plane or the number line as some might want to call it, we need to give it a name. This flat horizontal plane in 3D math is usually referred to as the X-axis.
The Second Dimension or the Y-axis
No points for guessing what the plane that makes up the 2D Cartesian space of 3D math is called. It is normally referred to as the Y-axis. The Y-axis is simply the representation of the x-axis but in this case, it is placed vertically with its origin intersecting with the origin of the X-axis.
This gives a visual representation of a cross with the positive numbers on the Y-axis placed above the zero and the negative numbers set below the zero.
Locations Using the 2D Cartesian Coordinates.
Throughout this article, I have used the term plane. Which is layman’s terms is a flat surface with four edges. For the sake of 3D math, the plane is the surface where the X-axis and the Y-axis are laid on.
We know the X-axis and Y-axis in 3D math are just two intersecting lines that cross at the origin which intersects at a right angle in relation to each other. That leaves so much space on the plane that these axes do not touch.
So if we are to represent a location on the plane how would we do it? I would express that location as a point in relation to both the X and Y axes in the format (x,y) where x is the mark on the X-axis and y is the mark on Y-axis where imaginary lines emanate from that point cross the X and Y axes respectively.
The illustration below would describe that in a much better way.
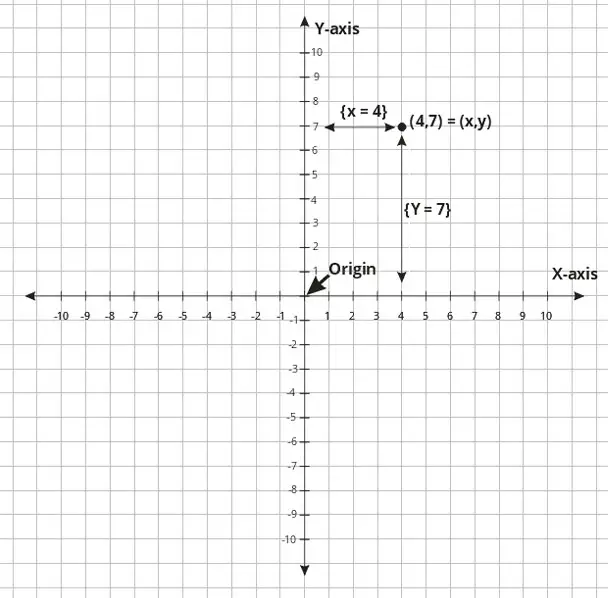
If we were discussing 2D graphics then we would not talk much further about this topic. It would be time to wrap up and call it a day. Nothing is ever that simple in my world so we must go ahead and talk about the third dimension that makes up the 3D worlds you find in 3D Math.
We will be continuing on in our series of 3D math with the introduction of the Z-axis and the components that make it possible to work in 3D worlds.
We will be discussing how the three dimensions relate to each other in 3D math and I will also revisit the issue above where we saw there could be a potential dispute with claiming the X-axis is placed horizontally.
We can then free our minds of this notion yet still continue to hang on to it for the sake of brevity.
Head on over to the second part in the series on the theory of 3D math for computer graphics.
Found this article interesting? Follow Brightwhiz on Facebook, Twitter, and YouTube to read and watch more content we post.