As we get started with the second part of our series on the 3D math that is essential for understanding 3D art, I would like to do a quick recap of what was discussed in our last article on the theory of 3D Math – Part 1.
This series on 3D maths seeks to help you get a general understanding of 3D scenes so that you can apply what you learn here in your future 3D projects.
For the basic 3D math needed to understand 3D Scenes in our last 3D math article, we talked about the 1D and 2D spaces and the coordinates of the Cartesian plane. We mentioned the idea behind the X-axis and the Y-axis and how they relate to each other.
We also talked about the four quadrants surrounding the point of intersection and how to determine the coordinates of any point on the Cartesian plane. In this article, we pick up from there and introduce more concepts.
Introducing the Third Dimension in 3D Math
From now on we will need to get comfortable with 3D spaces as we move away from the flat planes of 2D scenes.
Moving from 2D to 3D is done by adding a single dimension or the third dimension. We already live in a 3D world. Unfortunately growing up through the various education systems we found ourselves interacting with 2D representations of 3D worlds.
Be it an illustration in a book, a movie, television or graphics on your computer screen, where a 2D surface is used to represent the third dimension.
The next dimension we are dealing with from now on is also known in the industry as the Z-axis as seen in the illustration below.
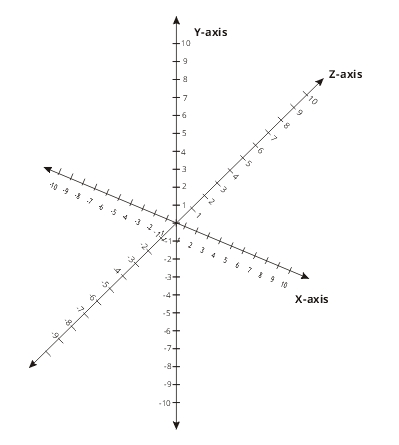
The Z-axis crosses the X-axis and the Y-axis at the same point the two axes intersect. Again the intersection is perpendicular to both of the X and Y axes. The addition of the Z-axis makes complete the 3D coordinate space in a 3D world.
In layman’s terms, we can say that it is customary to describe the X-axis pointing to the right and the Y-axis pointing up. These can be fairly standard most of the time. This is not always the case when dealing with the Z-axis. As we will see shortly, the Z-axis can either point forwards into the viewport or backward into the scene.
Again in a 3D scene, the theory mentioned above loses meaning because in a 3D scene these sets of axes can point in any direction other than vertically or horizontally. It is, therefore, safe to say that 3D worlds generally have no bounds as to the positioning of the axis.
The general and the more useful rule is to be aware of the relationship of the three axes to one another. They must each intersect with each other perpendicularly.
Locations Using the 3D Cartesian Coordinate Space
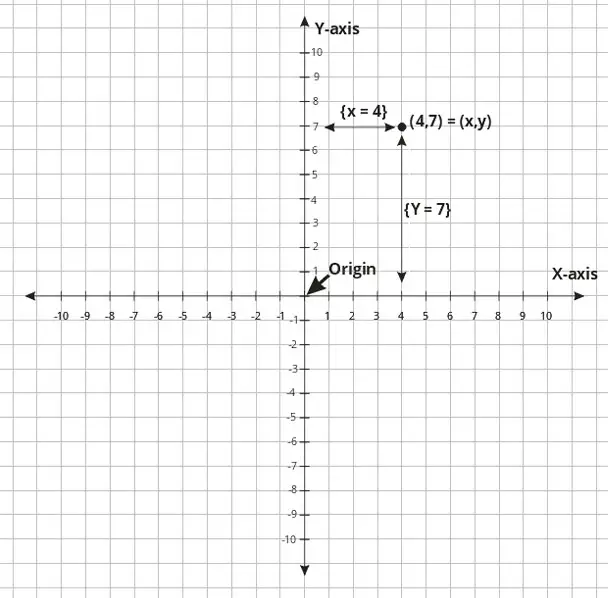
In the previous article as seen in this illustration, we saw how to express a point in a 2D world.
Based on the illustration above, it is fairly easy to guess how to express a point in a 3D space. You might have guessed right that we simply add the third point based on the Z-axis to fill in the third dimension of the world as shown below.
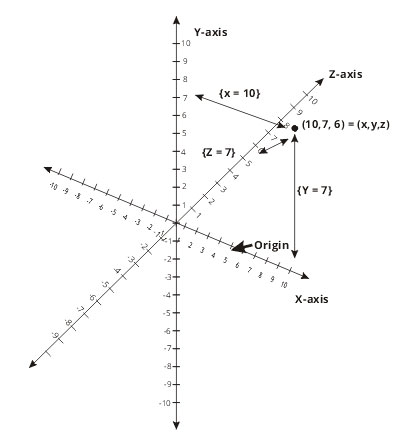
Now, this is not as straightforward as one would expect because as explained earlier, whichever orientation you place the X, Y plane. The relation between the X and Y-axes remains constant. Unfortunately, the Z-axis is not as consistent as we would like.
The Z-axis can either point forward or point backward. The direction in which the Z-axis points will greatly affect the value of the Z component when trying to find a point in a 3D space.
Normally in your program, this will never be a problem as long as you remain constant in the convention you pick for where you want your Z-axis to point.
The good news is the industry has determined a simple but innovative way to help the 3D artist determine the correct orientation and keep it constant.
Left-handed and Right-handed Coordinate Spaces
There is a clever way to determine the direction with which the Z-axis should point. It involves using your God-given hands and a little bit of flexibility. In 3D math, we call it the left-handed coordinate space or the right-handed coordinate space.
These human-handed coordinate spaces work with the 3D artist or programmer using certain fingers on their hands to represent the various axes. Irrespective of which hand you reference, the convention is to use the thumb to represent the X-axis. The index finger would then represent the Y-axis and the middle finger would then represent the Z-axis.
To represent a 3D coordinate space with your hand is simple:
- Hold out your left hand with palms facing forward.
- Stretch out your thumb until it is horizontal and pointing to the right. It should be relatively perpendicular to the index finger.
- Next, fold the last three fingers but stretch out your middle finger forward. Again make sure it is somewhat perpendicular to the index finger.
With all fingers stretched out, you now have the directions with which they point. Repeat the same with the right hand and you will notice the thumb on the right hand is pointing to the left.
To correct that, spin your right hand so that the thumb points right and your palm is facing towards you. You will notice the thumbs and index fingers of each hand are pointing in the same direction but the middle fingers are pointing in opposite directions.
The two illustrations below show it in more detail. This illustration below shows the left-handed coordinate space

This illustration below shows the right-handed coordinate space

Those are two possibilities of how the Z-axis works in the 3D coordinate space. You may choose to use either as long as you keep it consistent.
From here on we will be using the left-handed coordinate space. In our next part in this series on the theory of 3D math, we will look at the different or multiple coordinate spaces and discuss why they are important. The common multiple coordinate spaces in a 3D space include the World space, the Object space, the Camera space and Inertial space.
I have not yet read the first article in this series on the theory of 3D math then I would recommend you head on there and get started.
Found this article interesting? Follow Brightwhiz on Facebook, Twitter, and YouTube to read and watch more content we post.